SEMANA 1(30 DE SEPTIEMBRE, 3 DE OCTUBRE):
CLASE 1: Indicaciones generales.
CLASE 2: Comenzamos a estudiar los números complejos:
NÚMEROS COMPLEJOS
Forma Algebraica
z=a+ib donde a,b ∈ R
a--> Parte real Re(z)
bi-->Parte imaginaria Im(z)
UNIDAD IMAGINARIA
Igualdad de Números Complejos
Si z1 = a1+ ib1 ^ z2 = a2 + ib2
entonces, z1 = z2 <----> a1 = a2, ib1 = ib2
Suma de números complejos
Dado z1 = x1 + iy1 ^ z2 = x2 + iy2, entonces:
z1 + z2 = (x1 + x2) + i(y1 + y2)
Producto de complejos
Dado z1 = x1 + iy1 ^ z2 = x2 + iy2, entonces:
z1*z2 = (x1 + iy1 ) * ( x2 + iy2) = (x1*x2) + (ix2*y1) + (ix1*y2) + (iiy1*y2)
z1*z2 = (x1*x2 - y1*y2) + i(x2*y1 + x1*y2)
División de complejos
Dado z1 = x1 + iy1 ^ z2 = x2 + iy2, entonces:
Conjugado y Módulo de Z
Forman Polar de un complejo
z = r [cos(A) + isen(A)]
- Con estas fórmulas podemos transformar de forma binómica a forma polar y viceversa:
SEMANA 2(7 DE OCTUBRE, 10 DE OCTUBRE):
CLASE 3: Continuamos con el estudio de números complejos(Potenciación y Radicación), Realizamos trabajo en clase.
Potenciación

Radicación

CLASE 4:Entramos al tema de Funciones de Variable Compleja y Limites de las mimas:
- LÍMITES DE UNA FUNCIÓN COMPLEJA:
lim(z→zo)f(z)=L ↔∀ϵ>0;∃δ>0/|f(z)-L|<ε si 0<|z-zo|<δ
PROPIEDADES:

SEMANA 3(14 DE OCTUBRE, 17 DE OCTUBRE):
- CONTINUIDAD:
Se dice que f(z) es continua en z=zo si cumple:
i) ∃f(z0)
ii) ∃lim(z→zo)f(z)
iii) lim(z→zo)f(z)= f(z0)
SEMANA 2(21 DE OCTUBRE, 24 DE OCTUBRE):
- DISCONTINUIDAD:
Evitable:∃lim(z→zo)f(z) ^ ( ∄fzo) ó lim(z→zo)f(z) ≠ f(zo) )
Inevitable: ∄ lim(z→zo)f(z)
EXPONENCIALES COMPLEJAS O FÓRMULA DE EULER
Las funciones exponenciales complejas son solo de base e.
EXPONENCIALES COMPLEJAS O FÓRMULA DE EULER
Las funciones exponenciales complejas son solo de base e.
CLASE 6: Aprendimos sobre función exponencial, logarítmicas y sus propiedades.
LOGARITMOS COMPLEJOS
Sea z y w neros complejos distintos de cero
- e^[ln(z)]=z ; ln(e^z)=z+2Πk
- ln(zw)=ln(z)+ln(w)
- ln(z/w)=ln(z)-ln(w)
- Para todo número racional se cumple ln(z^ᾰ)=ᾰln(z)
- Exponencial compleja general, si z1 y z2 son complejos y z1~=0 entonces w=z1^z2 y w=e^[z2ln(z1)]
SEMANA 4 (21 DE OCTUBRE, 24 DE OCTUBRE)
CLASE 7: Realizamos ejercicios sobre el tema anterior y conocimos la funciones hiperbólicas.
CLASE 7: Realizamos ejercicios sobre el tema anterior y conocimos la funciones hiperbólicas.
FUNCIONES HIPERBÓLICAS
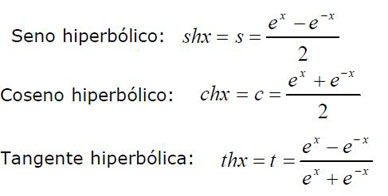
CLASE 8: Estudiamos las derivadas de funciones complejas.
DERIVADAS DE FUNCIONES COMPLEJAS
En esta clase se realizó el análisis de las derivadas de funciones de variable compleja. Se dice que existe la derivada de una función variable f (z), si:
- Las propiedades y reglas de derivación de funciones de variable real se aplican con las funciones de variable compleja.
SEMANA 5(28 DE OCTUBRE, 31 DE OCTUBRE):
CLASE 9: Se realizó trabajo en clase del tema anterior y comenzamos con un nuevo tema llamado funciones analíticas.
FUNCIONES ANALÍTICAS
Definición: f(z) es analítica en un Z inicial si y solo si f es derivable para todo z de algún disco D: |Z-Zo| < r .
También se enunciaron tres propiedades de las funciones analíticas:
i) Si la función f(z) = u(x,y) + iv(x,y) es analítica en algún dominio, entonces u y v satisfacen las ecuaciones de Cauchy-Riemann para todo (x,y) del dominio.
*Las Ecuaciones de Cauchy-Riemann (E.C.R.) son dos:
Si f(z) es analítica para todo z, entonces la función se denomina FUNCIÓN ENTERA.
CLASE 10: Complementando el tema anterior vimos: Funciones Armónicas:
FUNCIONES ARMÓNICAS
Sea f(z)=u(x,y)+iv(x,y)
Si u(x,y) y v(x,y) y sus primeras derivadas parciales son continuas, y cumplen las Ecuaciones de Cauchy-Riemann, entonces f(z) es analítica.
Si f(z) es analítica en un cierto dominio, entonces u y v son Armónicas, es decir cumplen con dos expresiones de las ecuaciones de Laplace.
- Si u y v son funciones armónicas, entonces se dice que u y v son conjugadas armónicas una de otra
.
ux=vy y uy=-vx (ECR)
BIBLIOGRAFÍA
RESUMEN TEORÍA: Números Complejos -Elena Álvarez Sáiz





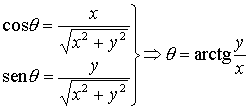

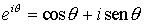

No hay comentarios:
Publicar un comentario