NOVIEMBRE

SEMANA 1(4 DE NOVIEMBRE, 7 DE NOVIEMBRE):

INTEGRALES DE FUNCIONES DE VARIABLE COMPLEJA

Integrales de línea  

 

• Se evalúan de manera similar a las integrales de linea de funciones reales de 2 variables.
• La novedad es las  integrales de Cauchy  y la existencia de derivadas de orden superior

INTEGRALES DE ORDEN SUPERIOR

Si la función de variable compleja que tenga antiderivada entonces se cumple:

                                              ∫f ( z ) d z = F ( z )+C

${\mathrm{ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; F}}^{\text{'}}\left(z\right)$ = f(z) 

INTEGRALES DE LÍNEA

Si gama es una curva suave a intervalos y f(z) es una función continua entonces existe una integral de línea sobre la curva gama.

i) x'(t) y  y'(t) son funciones continuas.

ii) x'(t) y  y'(t) no son simultáneamente igual a cero 

PROPIEDADES:

1. Sea f(x) una función continua y gama una curva suave o suave por intervalos, entonces:

2. La integral de la suma es igual a la suma de las integrales.

3. La constante que multiplique a la función de integración puede salir fuera de la integral

4. La integral de una función sobre una curva es igual al negativo de la integral sobre el negativo de la curva.

5. Si gama es una curva suave representada por z=z(t), para un t entre a y b, y f(z) es continua en C, entonces:

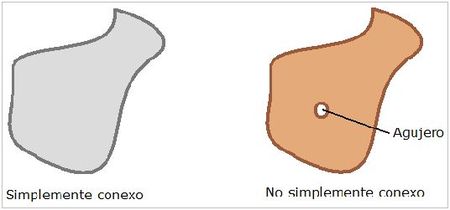
CONJUNTO SIMPLEMENTE CONEXO

Es aquel que solo contiene puntos de D, es decir no tiene huecos en su dominio.

PROPIEDAD 6: 

Si gama es una curva suave a intervalos de un z inicial a un z final en un dominio simplemente conexo, f(z) es analítica en D y tenga antiderivada en el dominio D, entonces:

INTEGRALES CERRADAS

Donde gamma es una curva cerrada(punto inicial es el mismo que el punto final), se evaluan según la definición de integral de línea.

CURVAS SIMPLES EN D

Gamma es una curva simple, si no presenta entrecruzamiento.

SIMPLE                             NO SIMPLE

SEMANA 2(11 DE NOVIEMBRE, 14 DE NOVIEMBRE):

PROPIEDAD 1:  Teorema de Integral de Cauchy

Sea una función analítica de D un dominio simplemente conexo y gamma una curva cerrada simple, entonces:

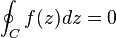
PROPIEDAD 2:

Si f(z) es analítica en un dominio simplemente conexo, la integral de f(z) es independiente de la trayectoria en D.

SEMANA 3(18 DE NOVIEMBRE, 21 DE NOVIEMBRE):

PROPIEDAD 3: Teorema de la Deformación.

Sea f(z) función analítica de D, excepto en Zo y sean gamma1 y gamma2 curvas cerradas simples entonces: 

PROPIEDAD 4: Integrales de Cauchy

Si f(z) es una función analítica en D, un dominio simplemente conexo y γ una curva cerrada simple que encierre a Zo.

COROLARIO:

PROPIEDAD 5: 

Formula de la integral de Cauchy para derivadas superiores.

COROLARIO:

SUCESIONES Y SERIES DE VARIABLES COMPLEJAS

Las sucesiones y series de variables complejas cumplen  propiedades similares a las sucesiones y series  de variable real a excepción de la serie de Laurent.

SUCESIONES

Es una función de los naturales sobre los complejos: 

Por ejemplo: 

 

Los elementos de tal sucesión serían:    

Una sucesión compleja se expresa así:  

Propiedades

    1. Si  para cada positivo n y si L = a + ib, entonces:

 

     Suponiendo que entonces:

    2.  

    3.  

    4.  

    5.   

CONVERGENCIA Para que una sucesión sea convergente debe cumplir:
 
SERIESUna serie es la suma de los elementos de una sucesión, esta se expresa así:

• Sucesión:  =

• Serie:         

La convergencia de la serie compleja se determina a través de las series reales que la componen.

Propiedades:Sea  se puede expresar:

1. converge si y solamente si  convergen
2. Si converge a "a"  y converge a "b" entonces:  converge a  "a+bi".
3. Si  converge, entonces . De esta propiedad también se puede decir:

SEMANA 4(25 DE NOVIEMBRE, 28 DE NOVIEMBRE):

CRITERIOS DE CONVERGENCIA DE SERIES

Criterio de la raíz                        
    

k<1 La serie converge.

k>1 la serie diverge.

k=1 el criterio no define nada.

Criterio de D'Alembert (Criterio del Cociente)

L>1 La serie converge.

L>1 la serie diverge.

L=1 el criterio no se decide

Criterio de Rabaae 

Se utiliza cuando ya no se puede aplicar el criterio de D'Alembert.

t>1 La serie converge.

t<1 la serie diverge.

t=1 el criterio no se decide

Criterio de Comparación

Viernes 28 se rindió el examen bimestral.